AGC005 B - Minimum Sum - ツバサの備忘録

解法

$i$ 番目の数字、 $a_{i}$ が採用される区間について調べてみます。
$l \leqq i \leqq r$ となる区間 $[l,r]$ について、 $a_{i}$ がその区間の最小値になるには、 $i\neq j$ かつ $l \leqq j \leqq r$ となる任意の $j$ について、 $a_{i} \lt a_{j}$ が成り立たなければなりません。
こうなるような $l$ の候補の最小値、 $r$ の最大値を求めてみます。
これが計算できれば、 $a_{i}$ が最小値となる区間の個数を利用して、
$a_{i} (i - l + 1)(r-i+1)$
という計算をすべての $i$ について行い、その和を取れば答えとなります。
$l$ は、 $a_{i} \gt a_{l-1}$ となるような $l$ の最大値、 $r$ は $a_{i} \gt a_{r+1}$ となるような $r$ の最小値です。
このままでは、一見簡単に求めるのが難しいように見えます。しかし、上のような条件を満たす $l,r$ が存在しない場合、すなわち $a_{i}$ が区間全体における最小値だった場合は、問答無用で $l$ は区間の左端、 $r$ は区間の右端になります。このことを利用します。
例えば、下のような $N=8$ の数列について考えてみます。

f:id:emtubasa:20190318231518p:plain

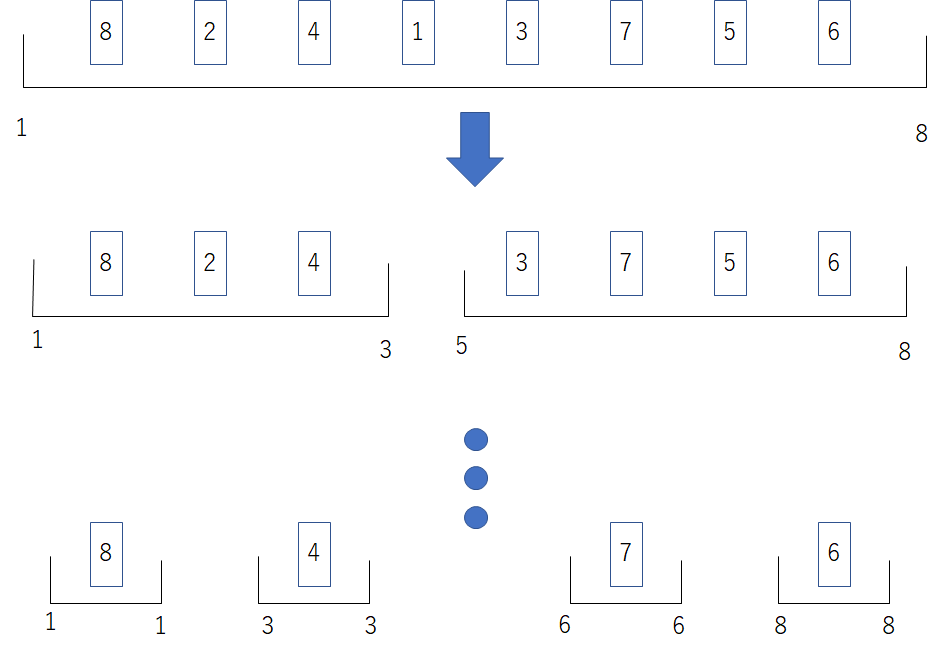
最初、区間全体を見ます。
$[1,8]$ の区間にある $a_{i}$ の最小値はもちろん $1$ になります。
ということで、 $i = 4,l = 1,r = 8$ として、 $a_{i} (i - l + 1)(r-i+1)$ を計算すると、
$1 \times 4 \times 5 = 20$
となります。
$1$ が絡む区間はすべて見終わったので、これを含まないような区間を調べます。すると、区間がちょうど2つに分かれます。
$[1,3]$ と $[5,8]$ です。
この新しくできた2つの区間について、それぞれの区間の中での最小値と、その位置を調べます。
前者は、 $i = 2,a_{i} = 2$ で、後者は $i = 5,a_{i} = 3$ です。
同じように $a_{i} (i - l + 1)(r-i+1)$ を計算してあげると、それぞれ
$2 \times 2 \times 2 = 8$
$3 \times 1 \times 4 = 12$
となります。
これで、 $2$ および $3$ が絡む区間を見終わったので、また区間を分けていきます。もし、最小値が端にある(今回の $[5,8]$ のような)パターンについては、新しい区間は1つしかうまれません。
この操作を、最終的に区間の幅が1になるまで繰り返していきます。
こうして、 $a_{i} (i - l + 1)(r-i+1)$ を計算していって全ての総和を取れば、答えがでてきます。
区間の最小値を取り出すのは、RMQを利用します。配列のインデックスは、ペアか何かで持たせておけば大丈夫です。

操作をまとめると、はじめは $l = 1,r = N$ として、
$[l,r]$ について、その区間内の最小値とそのインデックス $a_{i} ,i$ を探します。そして、
$a_{i} (i - l + 1)(r-i+1)$
を計算します。その後、
$[l,i-1]$ と $i+1,r]$ の新しい区間について、同じことを繰り返していきます。
そして、計算した $a_{i} (i - l + 1)(r-i+1)$ の総和を取れば答えになります。
調べたい区間をペアで管理し、新しく調べたい区間が出てくるたびにキューかスタックに格納していき、1つの区間を調べ終わったらまたそこから区間を1つ取り出していく、というようにすると、いい感じに調べることができると思います。

感想

てこずりました。ある数字が加算される(区間の最小値になる)条件と個数を調べていくのだろうな、とは思ったのですが、それを調べる方法がなかなか思いつきませんでした。
思考の過程としては、まず $a_{i}$ が最小値になるときのことを考えると、その区間 $[l,r]$ は、一定の場所までは区間を広げても常に成り立ち、一回条件を満たさなくなるとそれ以降区間をどれだけ広げても再び最小値になることはないことを確認します。すると、その区間が一番広い場所を探すことができれば、 $a_{i}$ が最小値になる回数がわかるので、 $a_{i} (i - l + 1)(r-i+1)$ を計算するだけでよいことになります。あとは、一番広くなる区間を探すだけなのですが、最初は $a_{i}$ を昇順に見ていってうまく処理できないかということを考えていました。結局それで調べる方法が思いつかなかったので悩んでいると、逆に、ある区間に対しての最小値を求めれば、その区間が答えになる、ということに気づいたので、上のような解法を思いつきました。