AGC26 - ツバサの備忘録

二回目のAGCでした。

A - Colorful Slimes 2

提出コード
まず入力時に、どの色のスライムがいるかを調べます。前から順番にスライムをチェックしていって、一個前のスライムと色が同じだったらその都度色を現時点で使ってない色に変えていけば、最短手数で合体しないスライム達ができあがります。
色を変えた回数を数える変数がbool型になっていて、時間が吸い取られました…自分のレート帯においてこれは本当に痛手でした。

B - rng_10s

提出コード(時間外)
考察はある程度までいったのですが、最後のつめが甘いのと、知識が足りない問題でした。
すぐに答えがわかる条件は3つあり、

$B>A$ のときNo(初日から買えないため)
上記の条件を除き、 $B>D$ のときNo(いつか供給がおいつかなくなるため)
上記の条件を除き、 $C \geqq B$ のときYes(買えなくなる前に必ず供給されるため)

というものです。自分は、 $B>D$ という条件について、 $B>D+$ 現在の本数、という条件にしていたため、複雑化してしまいました。
次に、すぐに答えがわからない条件、すなわち上の3つのパターン以外の時に、ジュースが買えなくなる条件はどうなるか、という問題について考えます。
$B \leqq A,B \leqq D, C\lt B$ という条件のもとでジュースが買えなくなるのは、

夜の時点での残り本数が、 $C$ より多いが、次の日にジュースを買うことはできない( $B$ より小さい)

という状況です。逆にいうと、残り本数がBより少ない時に入荷を必ず行えば、ジュースを買い続けることができます。また、この状況について考えるとき、夜の時点で残り本数が $B$ より多い時、夜に入荷はせず、次の日に $B$ 本買う、という作業しか発生しないため、 $B$ で割ったあまりのみを考えていいことがわかります。すると、
残り本数 $> C$
という条件に置き換えることができます。

ジュースを買い続けることができるとき、夜の時点での残り本数は、どこかでかならず初日の夜と同じになり、それ以降はループします。なので、一番厳しい条件である、残り本数を $B$ で割ったあまりの最大値だけについて調べ、その時でも $C$ 以下であれば、答えがYesになります。つまり、
残り本数のとりうる最大値 $\leqq C$ ならばYes
です。
さて、残り本数を $B$ で割ったあまりの最大値についての調べ方を考えます。
$A$ を $B$ で割ったあまりを $a$ 、 $D$ を $B$ で割ったあまりを $d$ とします。
ある日の残り本数は、その前日の残り本数に $d$ を加えて、 $B$ で割ったあまりになります。最初に $C$ 以下となるべき日の残り本数は、 $a$ です。
残り本数の最大値を、図を使って考えてみることにします。 $B$ で割ったあまりのみを考えるので、ある円について、円周上に $B$ 個の点を置き、それぞれの点に時計回りに0から $B-1$ までの数字をつけてあげます。つまり、ある点の数字に1足すと時計回りに1つ進み、 $B-1$ に1を足すと0になるような円を考えます。このとき、 $a$ をスタート地点として $d$ ずつ進んでいったときに通れる点の中で、一番数字が大きい点はどこか？という問題になります。

f:id:emtubasa:20180715233345p:plain — $d=2$ 、 $B=8$ のとき

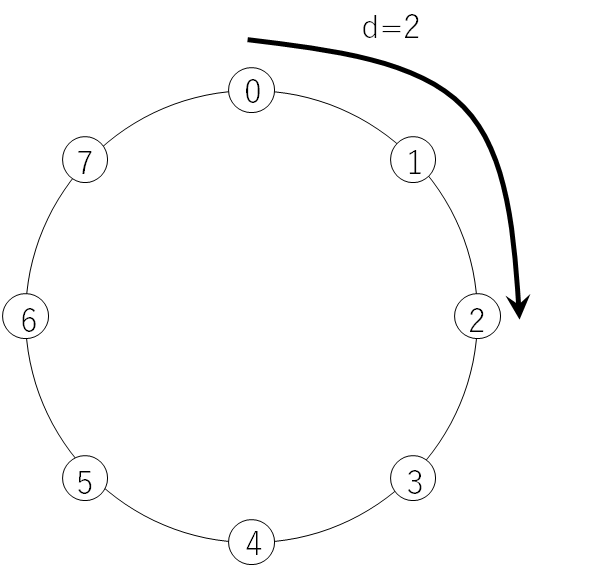
では、あらためて残り本数のとりうる最大値を求めていきましょう。
わかりやすくするために、スタート地点が0の時をまず考えます。
スタート地点に戻ってくるために必要な移動回数は、 $d$ と $B$ の最小公倍数を $l$ として、
$\frac{l}{d}$ 回
となります。(移動回数と $d$ をかけたものが $B$ の倍数になれば、 $B$ で割ったときのあまりが0になり、スタート地点に戻ります。 $B$ の倍数になる最小の数字は、最小公倍数そのものです。)また、スタート地点に再びもどってくるまでに、ほかの地点に2回以上訪れることはありません。なぜなら、もし2回以上訪れると仮定したとき、その地点をスタート地点とすると、1ループが上記の回数未満でおこっていることになり、矛盾するからです。

0をスタート地点としたときの、残り本数のとりうる最大値を、二つのパターンにわけて考えます。 $d$ と $B$ が互いに素であるときと、そうでないときです。

* $d$ と $B$ が互いに素であるとき
$l = d×B$
となるので、 $B$ 回移動すると、1回のループがおこります。ですが、先ほど述べたように、1回のループでは同じ点を1回しか訪れないため、全ての点に1回ずつ訪れていることになります。
このとき、訪れる点の中で一番大きい数字はというと、0から $B-1$ の中での最大はもちろん
$B-1$
になります。

* $d$ と $B$ が互いに素でないとき
$B$ と $d$ の最大公約数を $g$ と表記すると、 $l$ は次のように表現できます。
$l = \frac{B×d}{g}$
なので、 $d$ ずつ移動していくと、1ループまでに $\frac{B}{g}$ 回移動することになります。
1回のループでは同じ点を1回ずつしか通らないため、通る点の数字のパターンは次のように置き換えることができます。
0からスタートして、ある間隔 $p$ だけ $\frac{B}{g}$ 回移動したときに、ちょうど1周して0に戻るような $p$ を求めれば、 $p$ の倍数が、 $d$ ずつ移動したときに通る点の数字と同じになります。 $p$ はすぐに求まります。 $\frac{B}{g}$ 回移動したときにちょうど1周して0に戻るには、移動した距離の合計が $B$ になるようにしなければならないので、
$B = p × \frac{B}{g}$
より、
$p = g$
となります。
さて、 $g$ ずつ移動して、1回ループしたときに通る点の数字の中で最大のものはいくつでしょうか？答えは次のようになります。
$B-g$

以上で、0がスタート地点のときの、残り本数のとりうる最大値が求まりました。 $d$ と $B$ が互いに素のとき、 $g$ は1になるので、互いに素であっても最大値は $B-g$ と表記できるようになります。
では、最後にスタート地点が0ではなく $a$ だったときについて考えます。
例えば、 $a = g$ だったとき、スタート地点は $g$ だけずれますが、通る点の数字は $g$ の倍数なので、スタート地点が0のときと同じです。
同様にして、 $a > g$ だったとき、スタート地点は $a-g$ のときを考えるのと同じになります。これをくりかえすと、 $a$ を $g$ でわったときのあまりをスタート地点にした場合の最大値を求めればよくなります。
$a$ を $g$ でわったときのあまりを $a'$ と書くことにします。このとき、 $a'\lt g$ であることは明らかです。よって、求めたい最大値は $B-g+a'$ になります(先ほどの条件より、この値がBを超えることはないので、これが最大値になります)。
長くなりましたが、最後の条件は次のようになります。
$B-g+a' > C$ のときNo
最初の条件とあわせて、
$\left\{ \begin{array}{} B>A のときNo\\ 上記の条件を除き、 B>D のとき　No\\ 上記の条件を除き、C \geqq B のとき　Yes\\ 上記の条件を除き、B-g+a' > C のとき　No\\ それ以外のとき　Yes \end{array} \right.$
となります。
今回もやまさん(@yamasangamasan)にすこし解説してもらいました！数学系に強い人、うらやましいですね～。

C - String Coloring

提出コード(時間外)
最初読んだときに、これICPCのD問題っぽい！と思ってとりあえず全探索したのですが、通るわけありませんでした…その後はB問題に戻ったので、解けませんでした。
解法としては、文字列を前半と後半に分けて、後半だけ前後反転した後に、赤と青の色分けをすべてのパターン行い、その文字列のペアを、そのペアの出現回数とともに前半と後半それぞれのマップに格納します。そして、全探索が終わったら、前半にある文字列のペアが、後半にもあるかどうかを調べ、あったときにはその出現回数の積をカウントしていきます。調べおわったらカウントした数が答えになります。
半分にわけて全探索は有名らしい(?)ですが初めてだったので歯が立ちませんでした…

D以降は問題を見ていないので省略させていただきます。

というわけでまだまだ実力不足感が否めないので、数をこなして水色になりたいですね！